 > Departamento de Engenharia Química > > Mestrado Integrado em Engenharia Química > > Integração e intensificação de processos > > Shell and Tubes Heat Exchangers > > **Docente** **Responsável:** > > Nuno Manuel Clemente de Oliveira > > **Integrantes** **do** **grupo:** João Victor Vieira > Matteo Gecchele > **Introduction** **&** **Structure** > > The most common type of heat exchanger is the shell-and-tube, usually > used in a lot of industrial applications. This type of heat exchanger > has large number of tubes, sometimes several hundred, packed in a > shell with their axes parallel to that of the shell. The heat transfer > takes place between two fluid, one flowing inside the tubes and one > flowing outside the tubes through the shell. Baffles are commonly > placed in the shell to force the shell-side fluid to flow across the > shell to enhance heat transfer, to maintain uniform spacing between > the tubes and, also in order to maintain the turbulent flow inside the > exchanger. The baffle spacing is usually not greater than a distance > equal to the inside diameter or closer than a distance equal to > one-fifth the inside diameter of the shell. > > Usually the shell-and-tube heat exchangers have large size and weight, > and for this reason they are not using in automotive and aircraft > applications. At both ends of the shell, the tubes open to some large > flow areas, called headers, where the tube-side fluid accumulates > before entering the tubes and after leaving them. >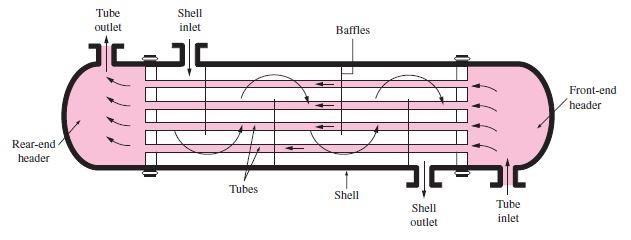 > > Shell-and-tube heat exchangers are further classified according to the > number of shell and tube passes involved. Heat exchangers in which all > the tubes make one U-turn in the shell, for example, are called > one-shell-pass and two-tube-passes heat exchangers. Likewise, a heat > exchanger that involves two passes in the shell and four passes in the > tubes is called a two-shell- passes and four-tube-passes heat > exchanger. 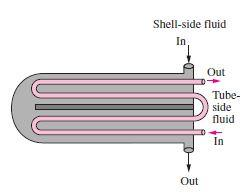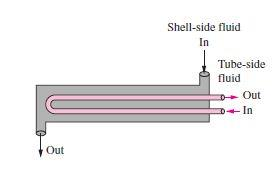 > **Operation** **principle** > > In order to calculate the temperature difference ∆𝑡 in a 1-2 > exchanger, it is necessary to make some assumptions: > > 1\. The shell fluid temperature is an average isothermal temperature > at any cross section > > 2\. There is an equal amount of heating surface in each pass 3. The > overall coefficient of heat transfer is constant > > 4\. The specific heat of each fluid is constant 5. The flowrate of > each fluid is constant > > 6\. There are not phase change (evaporation or condensation) in a part > of the exchanger > > 7\. Heat losses are negligible > > The overall heat balance where ∆𝑡 is the true difference of > temperatures, is: > > 𝑄 = 𝑈𝐴∆𝑡 = 𝑊𝐶(𝑇 − 𝑇 ) = 𝑤𝑐(𝑡2 − 𝑡1) where U is the heat transfer > coefficient and A is the surface of contact. > > Shell-and-tube heat exchangers are complicated devices and the > simplified approaches should be used with care. In fact, it is assumed > that the overall heat transfer coefficient U is constant throughout > the heat exchanger and that the convection heat transfer coefficients > can be predicted using the convection correlations. However, in some > practical application, the predicted value of U can exceed 30 percent. > Thus, it is natural to tend to overdesign the heat exchangers in order > to avoid unpleasant surprises. > > Heat transfer enhancement in heat exchangers is usually accompanied by > increased > > pressure drop, and this causes higher pumping power. Therefore, any > gain from the enhancement in heat transfer should be balanced against > the cost of the accompanying pressure drop. Also, some thought should > be given to which fluid should pass through the tube side and which > through the shell side. Usually, the more viscous fluid is more > suitable for the shell side (larger passage area and lower pressure > drop) and the fluid with the higher pressure for the tube side. > > Usually, it is convenient to relate the equivalent temperature > difference to the log > > mean temperature difference relation for the counter-flow case as > > ∆ 𝑙𝑚 = 𝐹∆ 𝑙𝑚,𝐶𝐹 where *F* is the correction factor**,** which depends on the geometry of the heat exchanger and the inlet and outlet temperatures of the hot and cold fluid streams. The > ∆𝑇𝑚,𝐶𝐹 is the log mean temperature difference for the case of a > counter-flow heat exchanger with the same inlet and outlet > temperatures. > > The correction factor *F* for a shell-and-tube heat exchanger is shown > in the figures below versus two temperature ratios *P* and *R* defined > as > > 𝑡2 − 𝑡1 𝑇 − 𝑡1 > > 𝑇 − 𝑇 𝑡2 − 𝑡1 > > where the subscripts 1 and 2 represent the inlet and outlet*,* > respectively. Note that for > > a shell-and-tube heat exchanger, *T* and *t* represent the shell-side > and tube-side temperatures, respectively. 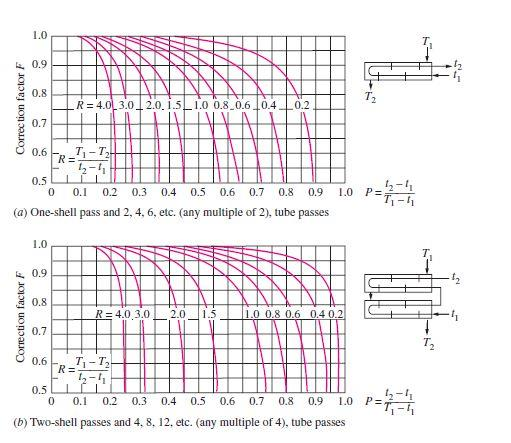 > **Factors** **that** **influence** **performances** *Fouling:* > > The performance of heat exchangers usually deteriorates with time as a > result of accumulation of deposits on heat transfer surfaces. The > layer of deposits represents additional resistance to heat transfer > and this causes a decrease of the rate of heat transfer in a heat > exchanger. The net effect of these accumulations on heat transfer is > represented by a fouling factor, which is a measure of the thermal > resistance introduced by fouling. > > For a shell-and-tube heat exchanger it possible to write the overall > heat transfer relation as > > 𝑈𝐴𝑠 = 𝑈𝐴𝑖 = 𝑈0𝐴0 = 𝑅 = ℎ𝑖𝐴𝑖 + 𝐴𝑖𝑖 + ln𝑈0𝐴0 𝑖) + 𝐴0 + ℎ0𝐴0 > > where 𝐴𝑖 = 𝐷𝐿 and 𝐴0 = 𝐷0𝐿 L are the areas of inner and outer > surfaces, and 𝑅,𝑖 and 𝑅,0 are the fouling factors at those surfaces. > > *Heat* *transfer* *rate:* > > The heat transfer rate is the most important parameter of a heat > exchanger. A heat exchanger should be capable of transferring heat at > the specified rate in order to achieve the desired temperature change > of the fluid at the specified mass flow rate. > > *Size* *and* *Weight:* > > The heat exchanger is better if it is smaller and lighter, in > particular, in the automotive and aerospace industries, where size and > weight requirements are most stringent. For this reason, > shell-and-tube heat exchangers cannot be used in this type of > application. Also, a larger heat exchanger normally carries a higher > price tag. The space available for the heat exchanger in some cases > limits the length of the tubes that can be used. > > *Material:* > > The thermal and structural stress effects need not be considered at > pressures below 15 *atm* or temperatures below 150*°C*. But these > effects are major considerations above 70 *atm* or 550*°C* and > seriously limit the acceptable materials of the heat exchanger. > > A temperature difference of 50*°C* or more between the tubes and the > shell will probably pose differential thermal expansion problems and > needs to be considered. In the case of corrosive fluids, we may have > to select expensive corrosion-resistant materials such as stainless > steel or even titanium. > > **Cost** > > The purchase cost of a shell and tube depends on the rear head type > and on the heat transfer > > area (size factor). The relationship between the purchase cost and the > size factor is > > represented in the graph below  > Both fluids are usually forced to flow by pumps or fans that consume > electrical power. The annual cost of electricity associated with the > operation of the pumps and fans can be determined from > > 𝑂𝑝𝑒𝑟𝑎𝑡𝑖𝑛𝑔𝐶𝑜𝑠𝑡 = 𝑃𝑢𝑚𝑝𝑖𝑛𝑔𝑃𝑜𝑤𝑒𝑟\[𝑘𝑊\] × 𝐻𝑜𝑢𝑟𝑠𝑜𝑓𝑂𝑝𝑒𝑟𝑎𝑡𝑖𝑜𝑛\[ℎ\] × > 𝑃𝑟𝑖𝑐𝑒𝑜𝑓𝐸𝑙𝑒𝑐𝑟𝑖𝑐𝑖𝑡𝑦\[\$ 𝑘𝑊ℎ\] > > where the pumping power is the total electrical power consumed by the > motors of the pumps and fans. > > Minimizing the pressure drop and the mass flow rate of the fluids will > minimize the operating cost of the heat exchanger, but it will > maximize the size of the heat exchanger and thus the initial cost. As > a rule of thumb, doubling the mass flow rate will reduce the initial > cost by half but will increase the pumping power requirements by a > factor of roughly eight. Typically, fluid velocities encountered in > heat exchangers range between 0.7 and 7 m/s for liquids and between 3 > and 30 m/s for gases. Low velocities are helpful in avoiding erosion, > tube vibrations, and noise as well as pressure drop. > > **Advantages**: > > *Size:* > > Shell-and-tube heat exchangers are capable of providing a larger > surface area for heat transfer to take place while having a shorter > length overall due to presence of multiple tubes. > > *Heat* *duty:* > > Shell-and-tube heat exchangers can handle higher temperatures and > pressures and hence higher heat duty. This is because besides > providing a higher overall heat transfer coefficient, additions can > also be made to negate thermal expansion effects and the thickness can > also be varied (more in the next point). > > *Versatility:* > > From the design point of view, shell-and-tube heat exchangers are the > most versatile of all heat exchangers. Being tubular in shape, heads / > closures of required shape and thickness can be used. The number of > tubes and tube pitch can be selected according to operating > conditions. Expansion bellows can be used to negate thermal expansion > effects, baffles if different cuts and spacings can be used to > influence the overall heat transfer coefficients and there's even > something called a floating head which can be added to negate thermal > expansion of the tubes. The number of passes on shell side and tube > side can be altered as well. > > **Disadvantages**: > > *Size:* > > This can also be a disadvantage as at lower heat duty, there are more > compact heat exchangers such as plate type exchanger. Also, the > absence of hairpin bends causes shell-and-tube heat exchangers to take > up more space than double pipe heat exchangers in some cases. > > *Maintenance:* > > Cleaning of tubes is difficult and fouling is always an issue when > overall heat transfer coefficient is addressed. This requires periodic > cleaning of the shell as well as the tubes. Cleaning tubes may be more > difficult if the pitch is triangular. > > **Utilities** > > The selection of utilities to be used in the shell and tubes tube > exchanger takes into > > account the type of industry in which it is being operated and the > desired parameters, such as the required power, thermal stability and > thermal capacity. > > *Cooling* *Water*: > > Cooling water is used to cool and/or condense currents. The cooling > water circulates inside heat exchangers. About 80% of the temperature > reduction is due to the evaporation of the cooling water and the > transfer of heat to the surrounding air. > > *Steam:* > > Steam is the most common heat utility used in the chemical industry > and can be used to power pumps, compressors and heat exchangers. Using > steam allows a more efficient heat source since the heat of > condensation of the steam is quite high, which translates into a high > yield per utility mass, at a constant temperature. Another reason is > that steam is non-flammable, non-toxic and inert to various process > fluids (more safe than other utilities like oil). > > **Conclusion** > > The simple design of a shell and tube heat exchanger makes it an ideal > cooling solution for a wide variety of applications and as a > consequence shell-and-tube heat exchangers are very popular and > commonly found in industrial use. > > **References** > > \[1\] Notes on Transfer Phenomena II, Professor Maria Graça Carvalho, > 2018/2019; > > \[2\] Warren D. Seider, University of Pennsylvania > > \[3\] Heat Transfer by Changel 2nd Edition > > \[4\] Heat Transfer by Holman 6th Edition
